隨著2013年4月13日的臨近,新一輪的多省聯考又一次拉開了序幕,相信學員們已進入到了緊張的備戰狀態之中。那么,在多省聯考的行測考試中,數量關系模塊依然是決定是否得到高分的關鍵性因素,也是眾多模塊中難度最大的部分。在離考試還有一個月的時間里,我們為考生提煉了數量關系模塊的快速解題法寶,以幫助大家高效地突破,沖出重圍。
一、掐準時間,選擇性做題
在考場上,很多考生根本沒時間做數量關系部分,而是采取直接蒙題的策略。其實,隨著近兩年數量關系部分整體難度的下降,60%-70%的考題都是中等及以下難度的題型。掌握好解題技巧,快速挑選出這些題目,可以獲得非常大的優勢。所以,對于這部分不能輕言放棄,最后做數量關系部分,只做會的,不會再選擇放棄。
二、基礎題型,熟練掌握解題技巧
延續往年趨勢,數量關系部分著重考察數學運算。對于過半的中等難度應用題,我們需要懂得識別題型、找對解題技巧,做到舉一反三。
1.代入排除法:適用多位數、年齡等問題。
【例1】一個三位數的各位數字之和是16,其中十位數字比個位數字小3,如果把這個三位數的百位數字與個位數字對調,得到一個新的三位數,則新的三位數比原三位數大495,則原來的三位數是多少?( )
A.169 B.358
C.469 D.736
【答案】B
【解析】多位數問題,考慮代入排除法。只有B選項滿足題意。因此,本題的正確答案為B選項。
【例2】有四個學生恰好一個比一個大一歲,他們的年齡相乘等于93024,問其中年齡最大的學生多少歲?( )
A.16歲 B.18歲
C.19歲 D.20歲
【答案】C
【解析】年齡問題,首選代入排除,注意代入的邏輯順序,從年齡最大的選項D開始代入。結合尾數法,可得只有C選項滿足題意。因此,本題的正確答案為C選項。
【點撥】當遇到特別棘手、無任何思路的復雜題型時,也可考慮代入排除法進行嘗試。
2.方程法:核心解題思想,重點把握不定方程。
【例3】超市將99個蘋果裝進兩種包裝盒,大包裝盒每個裝12個蘋果,小包裝盒每個裝5個蘋果,共用了十多個盒子剛好裝完。問兩種包裝盒相差多少個?( )
A. 3 B. 4
C. 7 D. 13
【答案】D
【解析】不定方程問題,考慮奇偶特性與尾數法的結合。設大包裝盒有x個,小包裝盒有y個,可列出方程:12x+5y=99。根據奇偶特性,12x為偶數,5y必為奇數尾數為5,12x的尾數為4,可得:x=2,y=15或x=7,y=3。又x+y>10,故x=2,y=15。兩種包裝盒相差13個。因此,本題的正確答案為D選項。
【點撥】不定方程,求整體的式子Ax+By=C,需要通過奇偶性分析5x或5y的尾數來湊解。
3.賦值法:適用經濟利潤及抽象問題。
【例4】某網店以高于進價10%的定價銷售T恤,在售出 后,以定價的8折將余下的T恤全部售出,該網店預計盈利為成本的:( )
A. 3.2% B. 2.7%
C. 1.6% D.不賺也不虧
【答案】B
【解析】抽象經濟利潤問題,考慮賦值法。設一件T恤的成本為10元,進貨了3件,故總成本為30元。每件T恤定價11元,賣出2件后開始打8折,故全部售出后可獲得:11×2+11×0.8×1=30.8元,盈利為30.8-30=0.8元。則盈利為成本的: ≈0.2+。因此,本題的正確答案為B選項。
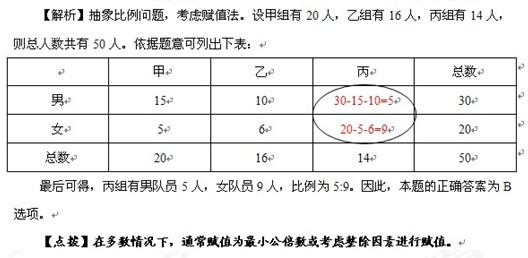
【例5】某調查隊男女隊員的人數比是3:2,分為甲乙丙三個調查小組。已知甲乙丙三組的人數比是10:8:7,甲組中男女隊員的人數比是3:1,乙組中男女隊員的人數比是5:3,則丙組中男女隊員的人數比是:( )
A.4:9 B.5:9
C.4:7 D.5:7
【答案】B
4.構造法:適用摸球題型及構造數列問題。
【例6】一個袋內有100個球,其中有紅球28個、綠球20個、黃球12個、藍球20個、白球10個、黑球10個。現在從袋中任意摸球出來,如果要使摸出的球中,至少有15個球的顏色相同,問至少要摸出幾個球才能保證滿足上述要求?( )
A.78個 B.77個
C.75個 D.68個
【答案】C
【解析】抽屜原理原型:摸球題型,特征為“保證+至少”,考慮“最不利情況+1”。題中要滿足有15個球的顏色相同,故最不利的情況是每種球摸出了14個,而不足14個的球只能摸到其最大值:即紅球14個、綠球14個、黃球12個、藍球14個、白球10個、黑球10個。最不利+1,根據尾數法為5。因此,本題的正確答案為C選項。
【例7】某單位組織黨員參加黨史、黨風康政建設、科學發展觀和業務能力四項培訓,要求每名黨員參加且只參加其中的兩項。無論如何安排,都有至少5名黨員參加的培訓完全相同。問該單位至少有多少名黨員?( )
A.17 B.21
C.25 D.29
【答案】C
【解析】抽屜原理+排列組合。首先,每名黨員從4項培訓中任選2項的種類數共有 =6種。要滿足6種選擇項下都有5名黨員,則最不利的情況是6種選擇項下只有4名黨員,故最不利+1,可得4×6+1=25名。因此,本題的正確答案為C選項。
【點撥】以摸球原型出發進行拓展,最近趨勢是抽屜原理結合排列組合進行綜合考察。
【例8】某單位2011年招聘了65名畢業生,擬分配到該單位的7個不同部門。假設行政部門分得的畢業生人數比其他部門都多,問行政部分得的畢業生人數至少為多少名?( )
A.10 B.11
C.12 D.13
【答案】B
【解析】求行政部分得的畢業生人數最少,判定屬于構造數列題,考慮列表法+方程法。行政部分得的畢業生人數最少,即其他部門分得的畢業生人數最多。設行政部分得的畢業生最少為x人,可列出下表:

依據上表可列出方程,x+6×(x-1)=65,解得x=10.1。最少為10.1人,取整為11人。因此,本題的正確答案為B選項。
【點撥】特別要注意題目中是否有“整數”、“互不相等”等限制條件,有或無會導致構造數列、列方程上的一些區別。
5.公式法:容斥問題、牛吃草問題、空瓶換水問題、植樹方陣問題、等差數列問題等。
(1)容斥問題核心公式:


(來源:華圖教育)

 分享到人人
分享到人人 分享到QQ空間
分享到QQ空間






























